A hybrid genetic algorithm to the program optimization model based on a heterogeneous network

doi:10.23919/JSEE.2025.000063

Journal of Systems Engineering and Electronics ›› 2025, Vol. 36 ›› Issue (4): 994-1005.doi: 10.23919/JSEE.2025.000063

• • 上一篇

收稿日期:2022-11-11 出版日期:2025-08-18 发布日期:2025-09-04

A hybrid genetic algorithm to the program optimization model based on a heterogeneous network

Hang CHEN¹(), Yajie DOU¹^,*(), Ziyi CHEN¹(), Qingyang JIA¹(), Chen ZHU²(), Haoxuan CHEN²()

¹ College of Systems Engineering, National University of Defense Technology, Changsha 410073, China
² College of Military Basic Education, National University of Defense Technology, Changsha 410073, China

Received:2022-11-11 Online:2025-08-18 Published:2025-09-04
Contact: Yajie DOU E-mail:hangchen_nudt@163.com;yajiedou_nudt@163.com;chenziyinudt@163.com;cassie_qing@163.com;zhuchen0923@163.com;chx15111159506@163.com
About author:
CHEN Hang was born in 1999. He received his B.S. degree from National University of Defense Technology, Changsha, China, in 2022. He is pursing his M.D. degree in National University of Defense Technology. His research interests are system optimization and comprehensive integration technology. E-mail: hangchen_nudt@163.com

DOU Yajie was born in 1987. He received his Ph.D. degree in management science and engineering from National University of Defense Technology, Changsha, China, in 2016. He is currently an associate professor of College of Systems Engineering, National University of Defense Technology. His research interests are weapon alternative decision and effectiveness evaluation, system-of-systems architecting and engineering management, and portfolio decision analysis.E-mail: yajiedou_nudt@163.com

CHEN Ziyi was born in 1995. He received his Ph.D. degree from National University of Defense Technology, Changsha, China, in 2023. He is currently a lecturer of College of Systems Engineering, National University of Defense Technology. His research interests are complex systems and system portfolio selection and optimization.E-mail: chenziyinudt@163.com

JIA Qingyang was born in 1998. She received her B.M. degree in financial engineering from Hunan University, Changsha, China, in 2020. She is currently pursuing her Ph.D. degree in management science and engineering with National University of Defense Technology. Her research interests is portfolio decision analysis. E-mail: cassie_qing@163.com

ZHU Chen was born in 2003. She is an undergraduate student in National University of Defense Technology, Changsha, China. Her research interests are defense acquisition and systems engineering.E-mail: zhuchen0923@163.com

CHEN Haoxuan was born in 2002. He is an undergraduate student in National University of Defense Technology, Changsha, China. His research interests are defense acquisition and systems engineering.E-mail: chx15111159506@163.com
Supported by:
This work was supported by the National Natural Science Foundation of China (7247011890; 72431011).

摘要/Abstract

Abstract:

Project construction and development are an important part of future army designs. In today’s world, intelligent warfare and joint operations have become the dominant developments in warfare, so the construction and development of the army need top-down, top-level design, and comprehensive planning. The traditional project development model is no longer sufficient to meet the army’s complex capability requirements. Projects in various fields need to be developed and coordinated to form a joint force and improve the army’s combat effectiveness. At the same time, when a program consists of large-scale project data, the effectiveness of the traditional, precise mathematical planning method is greatly reduced because it is time-consuming, costly, and impractical. To solve above problems, this paper proposes a multi-stage program optimization model based on a heterogeneous network and hybrid genetic algorithm and verifies the effectiveness and feasibility of the model and algorithm through an example. The results show that the hybrid algorithm proposed in this paper is better than the existing meta-heuristic algorithm.

Key words: program optimization, heterogeneous network, genetic algorithm, portfolio selection

. [J]. Journal of Systems Engineering and Electronics, 2025, 36(4): 994-1005.

Hang CHEN, Yajie DOU, Ziyi CHEN, Qingyang JIA, Chen ZHU, Haoxuan CHEN. A hybrid genetic algorithm to the program optimization model based on a heterogeneous network[J]. Journal of Systems Engineering and Electronics, 2025, 36(4): 994-1005.

图/表 13

参考文献 27

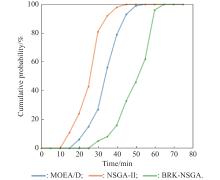
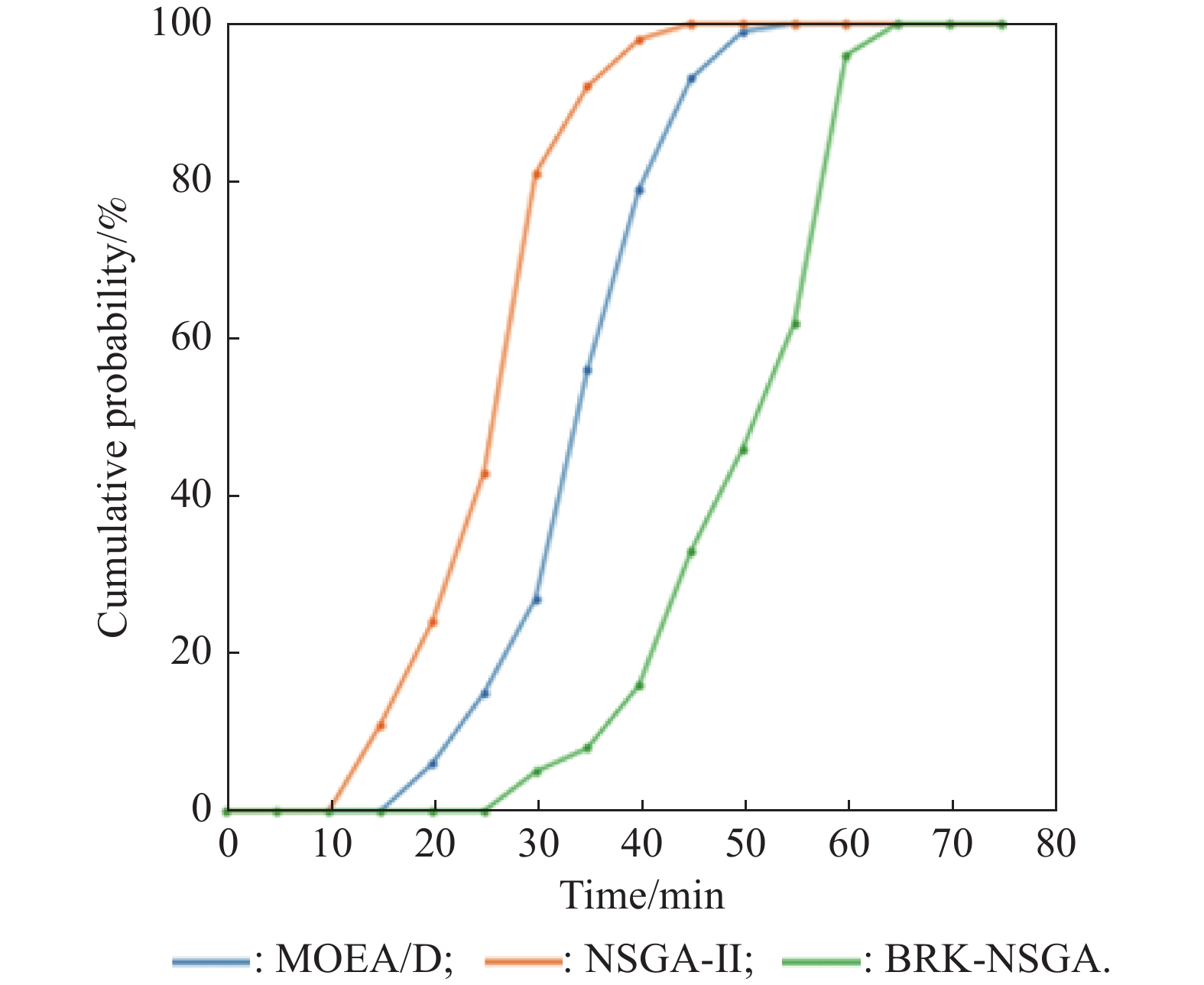
1	MARKOWITZ H Portfolio selection. Journal of Finance, 1952, 7 (1): 77- 91.
2	ZHANG X X, HIPEL K W, TAN Y J Project portfolio selection and scheduling under a fuzzy environment. Memetic Computing, 2019, 11 (4): 391- 406. doi: 10.1007/s12293-019-00282-5
3	MOHAGHEGHI V, MEYSAM M S, MOJTAHEDI M Project portfolio selection problems: two decades review from 1999 to 2019. Journal of Intelligent & Fuzzy Systems, 2020, 38 (2): 1675- 1689.
4	MAVROTAS G, MAKRYVELIOS E. An integrative review of project portfolio management literature: thematic findings on sustainability mindset, assessment, and integration. Operational Research, 2023, 23(3): 629−650.
5	ALVAREZ A, LITVINCHEV I S, LOPEZ F, et al Large-scale public R&D portfolio selection by maximizing a biobjective impact measure. IEEE Trans. on Systems, Man, and Cybernetics−Part A: Systems and Humans, 2010, 40 (3): 572- 582. doi: 10.1109/TSMCA.2010.2041228
6	FISHER B, BRIMBERG J, HURLEY W J An approximate dynamic programming heuristic to support non-strategic project selection for the Royal Canadian Navy. Journal of Defense Modeling and Simulation, 2015, 12 (2): 83- 90. doi: 10.1177/1548512913509031
7	ESHLAGHY A T, RAZI F F A hybrid grey-based k-means and genetic algorithm for project selection. International Journal of Business Information Systems, 2015, 18 (2): 141- 159. doi: 10.1504/IJBIS.2015.067262
8	MANISH K, MITTAL M L, GUNJAN S, et al A tabu search algorithm for simultaneous selection and scheduling of projects. Proc. of the Harmony Search and Nature Inspired Optimization Algorithms, 2019, 741, 1111- 1121.
9	BLAZEWICZ J, LENSTRA J K, KAN A Scheduling subject to resource constraints: classification and complexity. Discrete Applied Mathematics, 1983, 5 (1): 11- 24. doi: 10.1016/0166-218X(83)90012-4
10	KIM J A, KANG C B, HWANG I C A practical approach to project scheduling: considering the potential quality loss cost in the time-cost tradeoff proble. International Journal of Project Management, 2012, 30 (2): 264- 272. doi: 10.1016/j.ijproman.2011.05.004
11	KYRIAKIDIS T S, KOPANOS G M, GEORGIADIS, et al. MILP formulations for single and multi-mode resource constrained project scheduling problems. Computers & Chemical Engineering, 2012, 36(10): 369−385.
12	HEILMANN R A branch-and-bound procedure for the multi-mode resource-constrained project scheduling problem with minimum and maximum time lags. European Journal of Operational Research, 2003, 144 (2): 348- 365. doi: 10.1016/S0377-2217(02)00136-4
13	BUDDHAKULSOMSIRI J, KIM D S Priority rule-based heuristic for multi-mode resource-constrained project scheduling problems with resource vacations and activity splitting. European Journal of Operational Research, 2006, 178 (2): 374- 390.
14	LOVA A L, TORMOS M P, BARBER F. Multi-mode resource constrained project scheduling: scheduling schemes, priority rules and mode selection rules. Inteligencia Artificial, 2008, 10(30): 69−86.
15	SINGH A Resource constrained multi-project scheduling with priority rules & analytic hierarchy process. Procedia Engineering, 2014, 69, 725- 734. doi: 10.1016/j.proeng.2014.03.048
16	GERHARDS P, STURCK C, FINK An adaptive large neighborhood search as a metaheuristic for the multi-mode resource-constrained project scheduling problem. European Journal of Industrial Engineering, 2017, 11 (6): 774- 791. doi: 10.1504/EJIE.2017.089101
17	SEIFI M, TAVAKKOLI M. A new biobjective model for a multimode resource-constrained project scheduling problem with discounted cash flows and four payment models. International Journal of Engineering, 2008, 21(4): 347−360.
18	DELGOSHAEI A, ARIFFIN M K Pre-emptive resource-constrained multimode project scheduling using genetic algorithm: a dynamic forward approach. Journal of Industrial Engineering and Management, 2016, 9 (3): 732- 785. doi: 10.3926/jiem.1522
19	MIKA M, WALIGORA G, WEGLARZ J Tabu search for multi-mode resource constrained project scheduling with schedule-dependent setup times. European Journal of Operational Research, 2008, 187 (3): 1238- 1250.
20	ZHAI X, TANG Z, LIU Z, et al Sparse representation for heterogeneous information networks. Neurocomputing, 2023, 525, 111- 122. doi: 10.1016/j.neucom.2023.01.035
21	SHI C, LI Y, PHILIP S Y. A survey of heterogeneous information network analysis. IEEE Trans. on Knowledge and Data Engineering, 2017, 29(1): 17−37.
22	ZHANG X, WANG C T, SU Y S. A fast overlapping community detection algorithm based on weak cliques for large-scale networks. Web Search and Data Mining, 2017, 4(4): 218−230.
23	BEAN J. Genetic algorithms and random keys for sequencing and optimization. ORSA Journal of Computing, 1994, 6(2): 154−160.
24	ZHENG W, LIU Y, DOERR B. A first mathematical runtime analysis of the no dominated sorting genetic algorithm II. Proc. of the Genetic and Evolutionary Computation Conference Companion, 2022. DOI: https://doi.org/10.1609/aaai.v36i9.21283.
25	WEIR T. Generalized convexity and duality in mathematical programming. Bulletin of the Australian Mathematical Society, 1983, 27(3): 471−472.
26	HARRISON K R, ELSAYED S, GARANOVICH I L, et al A hybrid multi-population approach to the project portfolio selection and scheduling problem for future force design. IEEE Access, 2021, 9 (1): 2169- 3536.
27	WEIR T. Regression models for project expenditures. Proc. of the National Conference of the Australian Society for Operations Research , 2018: 271−290.

Instance	Program size	Objective dimension
Instance1	300	4
Instance2	400	4
Instance3	500	2
Instance4	500	3
Instance5	500	4
The planning horizon is 30 years

Method	Parameter	Range	Value
NSGA-II	Size	[100,500]	382
NSGA-II	Mutants	[0.1,0.4]	0.10
MOEA/D	Size	[100,500]	126
MOEA/D	Subproblems	[10,35]	20
BRK-NSGA	Size	[100,500]	151
	Elites	[0.1,0.5]	0.3
	Mutants	[0.1,0.4]	0.10
	Non-elite parent	[1,3]	2
	Elite parent	[2,8]	6

Instance	NSGA-II		MOEA/D		BRK-NSGA
Instance	Effective	Pareto	Effective	Pareto	Effective	Pareto
Instance 1	15.3	49.4	20.2	52.9	17.4	87.1
Instance 2	11.4	31.8	17.4	58.4	15.2	85.4
Instance 3	31.2	50.5	25.0	73.0	24.8	88.6
Instance 4	18.4	29.9	22.5	62.7	18.8	86.7
Instance 5	8.4	18.5	12.3	53.3	13.2	91.4

A hybrid genetic algorithm to the program optimization model based on a heterogeneous network

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 13

参考文献 27

相关文章 0

编辑推荐

Metrics

本文评价